インバータICを2個使う発振回路について実験しました。でもわからないことが多いです。前にやったシュミット・インバータの発振回路とどう違うのか、どう使い分けるのか知りたかったのですが、そこまで解明できませんでした。実験にあたっては、鈴木憲次著「トラ技オリジナルNo.2 製作研究 ディジタルIC回路の誕生」(CQ出版社) という本を参考にしました。

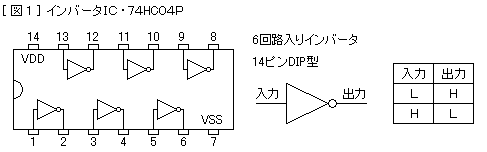
図1は6回路入りインバータIC・74HC04Pのピン接続図です。このページには他のインバータICも出てきますが、すべてピン接続は同じです。ICのメーカーはいずれも日立のもの (型番の最初にHDが付く) を用いました。
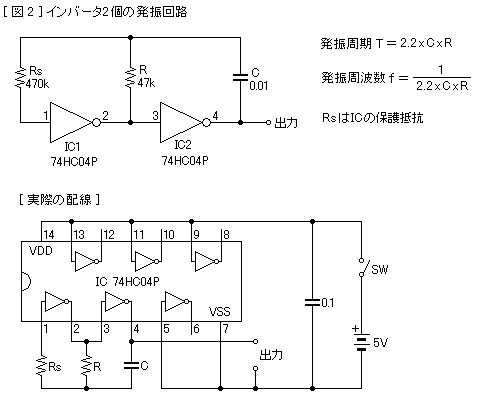
図2はインバータ2個の発振回路の基本回路図です。実際の配線では不使用のユニットの入力端子は電源プラスあるいはマイナスにつないでおきます。出力端子はオープンにします。電源電圧は5Vにしました。
発振周波数はCとRの大きさに反比例します。本には 1÷(2.2xCxR) という式が出ています。上の例ではC=0.01μF, R=47kΩですから周波数f=967Hzです。ただし保護抵抗Rsの値やその他の条件によって周波数は変動します。実際の発振周波数は930Hzくらいになりました。RsはIC1の入力に過大な電流が流れてICが壊れるのを防ぐためのものです。上記の参考書には、RsはRの10倍くらいにしなさいと書かれていましたので、ここでは470kΩにしました。でも雑誌等の製作記事を見ると抵抗値はまちまちです。Cが小さい場合はRsが省略されていることもあります。
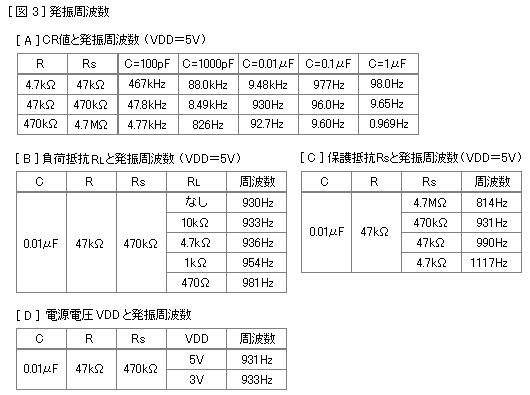
上記は回路定数をいろいろに変えて発振周波数を調べた結果です。表AはCR値による周波数の違いで、RsはRの10倍という条件にしています。つまりR=4.7kΩのときRs=47kΩ、R=47kΩのときRs=470kΩ、R=470kΩのときRs=4.7MΩです。Cが大きいときはだいたい先の計算式と合っているようですが、Cが小さくなるにしたがって周波数は下がってきます。C=100pFのときは、ICの入力容量や回路の浮遊容量の影響もあるのでしょうが、計算値の半分くらいになってしまいました。
表Bは負荷抵抗RLの値と周波数の関係です。IC2の出力端子とGND間にいろいろな値の抵抗をつないで周波数の変化を調べました。RLが小さいほど周波数は高くなります。シュミットインバータ発振回路と逆ですね。
表Cは保護抵抗Rsによる周波数の違いを調べたものです。Rに比べてRsが小さいと周波数が高くなります。ただしCが大きい場合はそれほど大きな違いにはなりません。
表Dは電源電圧VDDと周波数の関係で、5Vでも3Vでもほとんど変化しませんでした。この点は先のシュミットインバータ発振回路より安定しています。
発振回路の動作について書きます。本の請け売りですが。
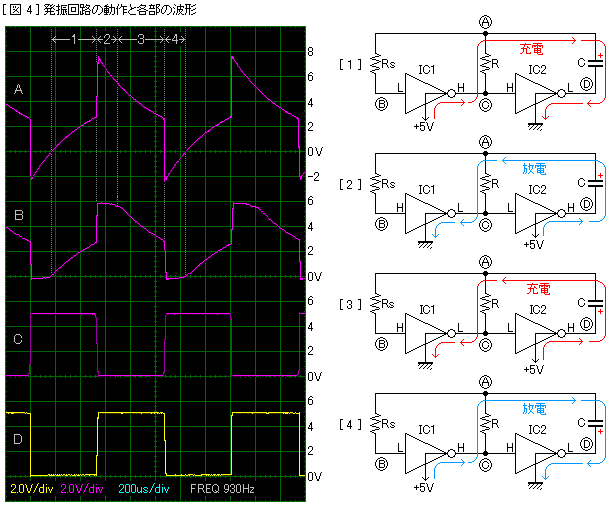
図4左は発振回路の各部分の波形図です。右は発振の1周期を4つに分けてそれぞれの動作を表した図です。最初の状態 (1) ではIC1の入力がL、IC1の出力とIC2の入力がH、IC2の出力がLになっています。このときは電源プラスからIC1の出力→R→C→IC2の出力→GNDへと電流が流れてCに充電します。
充電が進んでCのプラス側、すなわちA点の電位がICのスレッショルド電圧VTH (約2.5V) に達するとIC1の出力は反転してLになり、IC2の出力 (発振回路の出力) はLになります。これが2の状態です。このときは先と同じ経路を逆に電流が流れてCは放電します。2の期間の最初のところは電源電圧VDDにCの充電電圧がプラスされるので、A点の電位はGNDに対してVDD+VTHになることに注意してください。
Cに溜まっていた電気がすべて放電してもまだIC2の出力はHのままなので、電流はそのまま同じ方向に流れ続けます。このためCはさっきとは逆の極性に充電されます (図3の状態)。Cの電荷がゼロのときはA点の電位はVDDと同じですが、充電が進むにつれてだんだん下がってきます。VTHまで下がったところで出力が反転し、図4の状態になります。
4の期間の最初はCの両端の電圧がVTH (2.5V) ですので、A点はGNDレベルよりさらにVTH分だけ低いマイナスの電位になります。ここからCの放電が始まり、A点の電位は少しずつ上昇します。Cが空になると最初の1の状態に戻って引き続き逆極性での充電が始まります。
図4にはIC1の入力端子 (B点) の波形も掲げました。A点の電位は0V〜VDD以上の範囲で変化しますが、B点の電位は0V〜VDDよりわずかに大きいくらいの範囲にとどまっています。これはIC内部の保護ダイオードのはたらきによるものです。ICの入力にVDDを超える電圧、あるいは0V以下のマイナスの電圧が加わったときこのダイオードが導通してICに過大な電圧が加わらないように保護しています。しかしこの保護ダイオードに流せる電流には制限があり、HD74HC04Pのデータシートでは最大20mAとなっています。そのため外部に保護抵抗Rsを接続する必要性が生じます。
先に実験したようにこの発振回路ではRsの値によって発振周波数が変化します。そのようすをオシロの波形で確かめてみました。下に、Rsが470kΩ, 47kΩ, 4.7kΩのときのB点の波形図 (赤) を示します。いずれもCは0.01μF、Rは47kΩです。黄色は出力波形です。
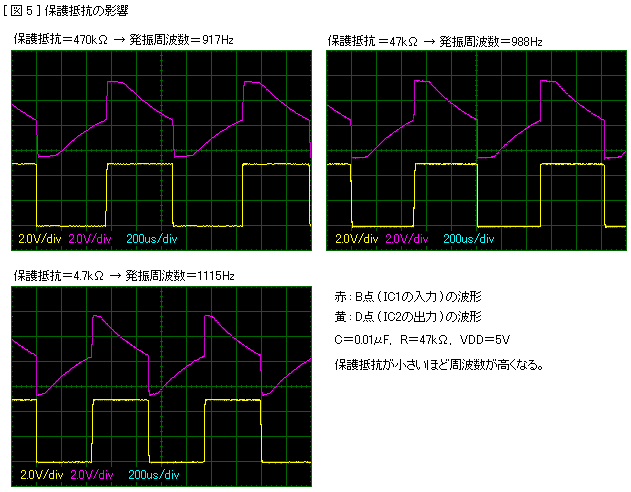
B点の波形 (赤) の平坦な部分がIC内部の保護ダイオードが導通している時間です。Rsが小さいほどB点の波形の平坦部分が短くなることがわかります。その分だけ発振周期も短くなり、周波数が高くなるものと思われます。なお、Rs=470kΩのときは図4と同じなのに周波数が917Hzと低くなっています。これはB点にオシロのプローブをあてると回路の状態が変化してしまうためです。図4では説明の都合上B点の波形図の横幅を少し縮めてA点の波形図に合わせました。
同じ発振回路でICだけを差替えた場合、発振周波数がどう変化するか調べました。
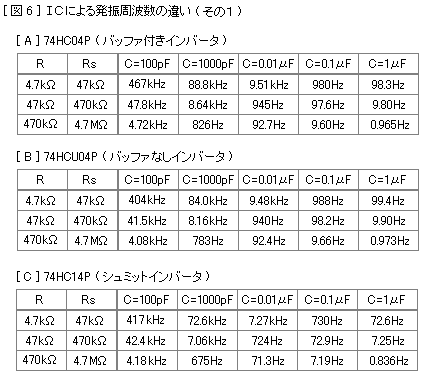
図6は、これまでの実験で使用したバッファ付きインバータ74HC04Pの他、バッファなしインバータの74HCU04P、シュミットインバータの74HC14Pを使用したときの周波数の比較です。シュミットインバータ2個をこの回路で使うと周波数が少し低くなります。周波数以外の相違点はよくわかりませんが、高い周波数での動作では74HC04Pより74HCU04Pの方が安定していると書いてある記事もあります。
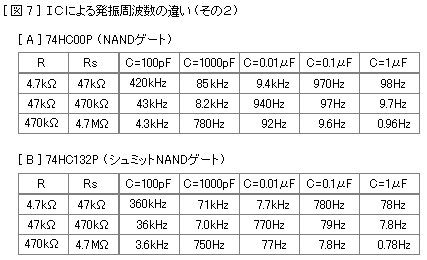
図7はNANDゲートの74HC00P、およびシュミットNANDゲートの74HC132Pを使った場合です。2つの入力を結ぶとインバータと同じ動作になります。これらのICを使った回路では出力周波数が細かく変動して安定しませんでした。そのため表中には概略の周波数を記してあります。
ここまではRsをRの10倍にして実験してきたのですが、試しにRsを1kΩにしてみたところ、NANDゲートICでも安定して発振するようになりました。ただ、上にも書いたように周波数は少し高くなります。Cが0.01μF以上では、10%くらい、1000pFのときは20%くらい、100pFのときは2倍くらいに上昇します。そもそも、なぜRsを高くする必要があるのでしょう。周波数が計算値からずれるだけのことならば、Rsを低くして安定に動作させた方がいいような気もしますが。
この発振回路もシュミットインバータ発振回路と同じように遊べますので、応用回路については別項「シュミット・インバータによる発振回路」を見てください。NANDゲートICを用いて発振のオンオフをコントロールできるのも同じです。これについては「シュミットNANDゲートICによる発振回路」をご参照ください。シュミットインバータ発振回路とまるっきり同じとは思いませんが、少なくともLEDピカピカとか電子ブザーで遊んでいる分には違いがわかりません。
出力のデューティ比を変更する回路だけ下に出しておきます。
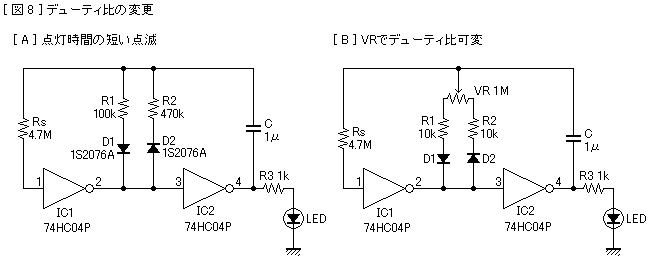
図9AはLEDが点灯時間の短い点滅動作をする回路です。図の定数で点滅周期は約0.7秒、点灯時間と消灯時間の比率は1:5くらいでした。Bはボリュームでデューティ比を連続的に変化させるもので、VRのスライダーがD1側へ行くほど点灯時間の短い点滅になります。
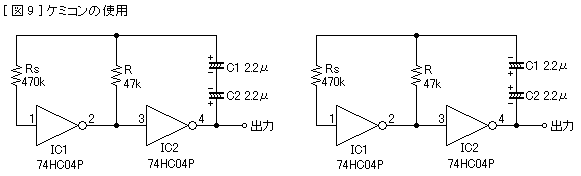
インバータ2個の発振回路ではコンデンサが両極性に充電されるので、ケミコンなど極性のあるコンデンサは使用できません。しかし雑誌の製作記事等では普通のケミコンを背中合わせに2個直列にして使ってあるものをときどき見かけます。図9の回路では2.2μFのケミコンを2個直列にしました。こうすると容量は半分の1.1μFになります。発振周波数は9.4Hzでした。ケミコンのこういう使い方は短時間の実験ならば問題ありませんが、長期間の使用に耐えるかどうかは不明です。このほかバイポーラケミコン (両極性ケミコン、無極性ケミコン) を使用する例も見たことがあります。